Types of Quadrilaterals - Squares, Rectangles, Trapezoids & More

Learn about the different types of quadrilaterals, from squares and rectangles to trapezoids and rhombuses. This guide provides definitions, properties, examples, and practice problems to help you master quadrilateral geometry.

What Is a Quadrilateral?

A quadrilateral is a four-sided shape, known as a polygon. The name comes from the Latin words “quadri,” meaning four, and “latus,” meaning side. This means all quadrilaterals have exactly four edges or sides.

Key Characteristics

Quadrilaterals have some key features:

Sides: They always have four straight sides.
Angles: The total of all inside angles in a quadrilateral is always 360 degrees.
Vertices: There are four corners (or vertices) where two sides meet.
Diagonals: A diagonal connects two non-adjacent vertices. Each quadrilateral has two diagonals.

Convex vs. Concave Quadrilaterals

Quadrilaterals can be split into two types based on their shape:

Convex Quadrilaterals: All angles are less than 180 degrees, and if you draw lines between points on the edge, they stay inside the shape. Examples are rectangles and squares.
Concave Quadrilaterals: At least one angle is greater than 180 degrees, making part of the shape cave inwards. An example would be an arrowhead shape.

Understanding these features helps us tell apart different types of quadrilaterals and see their special properties in geometry.

Why Are Quadrilaterals Important in Geometry?

Quadrilaterals matter a lot in areas like architecture, design, and engineering because they can do many things.

In architecture and design, we see many buildings use rectangular windows or square tiles since they fit well together without leaving spaces. These shapes help make structures strong and nice to look at.

We also run into quadrilaterals in everyday items like tables or bookshelves that usually have flat surfaces to save space and work well for us. Knowing about these shapes helps us understand how math fits into things we see around us!

Types of Quadrilaterals Explained

Parallelogram Properties and Examples

A parallelogram is a special kind of quadrilateral. It has four sides. In a parallelogram, the opposite sides are equal and run parallel to each other. This makes it stand out among different quadrilaterals. Plus, the opposite angles in a parallelogram are equal.

What is a parallelogram?

You can find parallelograms in everyday life! Think about window panes or floor tiles. These shapes show how this type of polygon works in real life.

Property	Description
Opposite Sides	Equal and parallel
Opposite Angles	Equal
Diagonals	Bisect each other but might not be equal

Rectangle Characteristics vs Parallelograms

Rectangles have some features similar to parallelograms, but they also have unique traits. A rectangle always has four right angles (90 degrees), and its diagonals are equal in length.

What makes a rectangle unique?

The main difference between rectangles and regular parallelograms is the right angles and diagonal lengths. Rectangles keep their area calculations based on width and height, while the perimeter adds all the side lengths together.

You see rectangles all around! Common examples are doors or computer screens that clearly show rectangular shapes.

Square Properties Compared to Rectangles & Rhombuses

A square is another special type of quadrilateral. It stands out because all its sides are equal in length. This makes it both a rectangle (with right angles) and a rhombus (with all sides equal).

How is a square different from rectangles/rhombuses?

Squares have symmetry along both diagonals. When you draw the diagonals inside the shape, they meet at right angles. This feature sets squares apart from regular rectangles or rhombuses, which may not share this property.

Squares are easy to spot in things like chessboards or dice!

Rhombus Features Distinct From Squares/Parallelograms

Rhombuses have adjacent sides that are equal but do not form right angles like squares do. A key characteristic of rhombuses is that their diagonals bisect at right angles.

What defines a rhombus?

Every rhombus shares qualities with squares and parallelograms, yet it keeps distinct differences through its angles and side relationships. You can see real-world examples in kite shapes or some crystal formations found in nature!

Trapezoids: Definition and Types

A trapezoid is a special kind of quadrilateral. It has one pair of parallel sides. These parallel sides are called the “bases.” The other two sides are known as the “legs.” This is what makes trapezoids different from other quadrilaterals.

Properties of Trapezoids

Trapezoids have some neat properties:

Parallel Sides: The bases are not just for looks; they create unique angles beside them.
Angle Sum: If you look at the angles on one side of the parallel sides, their total is 180°. So, if you know two of those angles, you can find the third one easily.

Isosceles Trapezoids

An isosceles trapezoid is a specific type of trapezoid where both legs are equal in length. Here are some important points:

Equal Legs: The non-parallel sides (legs) are the same length.
Equal Diagonals: The diagonals that connect opposite corners are also equal.
Base Angles: The angles next to each base match each other.

Real-world Examples

You can see trapezoids everywhere! Some examples include:

A traffic sign that looks like an upside-down trapezium.
Certain table designs use this shape to look nice.

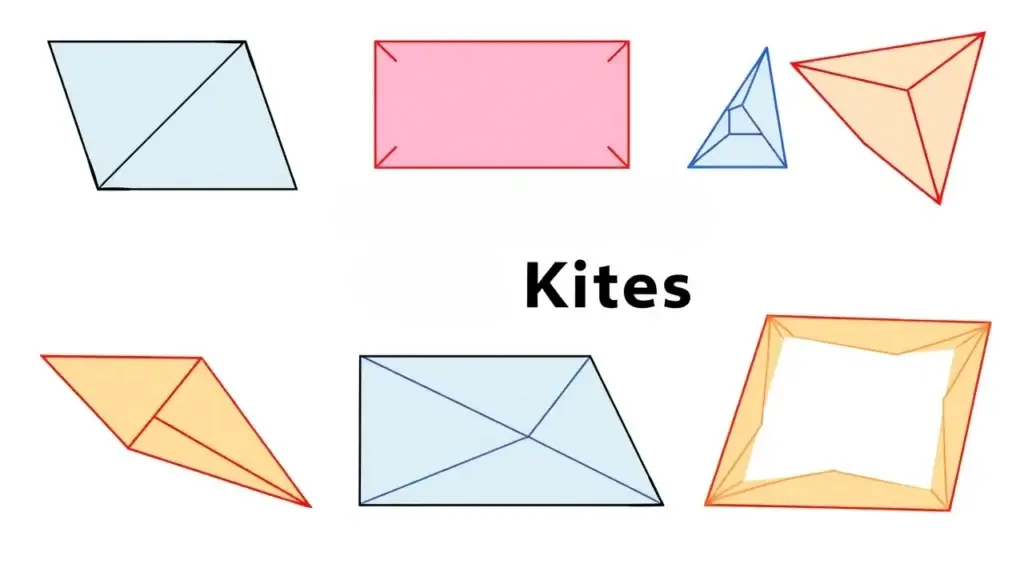
Kites: Definition and Properties

A kite is another fun type of quadrilateral. It has two pairs of adjacent equal sides. That means each pair includes two sides that meet at a corner.

Properties of Kites

Kites have some interesting features:

Diagonal Relationship: One diagonal cuts the other diagonal in half at a right angle.
Opposite Angles: One set of opposite angles in kites is equal.

Real-world Examples

You can find kite shapes in many places:

Diamonds used in jewelry look like kites due to their symmetry.
Decorative designs often feature kite shapes for added beauty.

Learning about these shapes helps us understand more about geometric figures we see every day!

Understanding Irregular Quadrilaterals

An irregular quadrilateral is a four-sided shape with no equal sides or parallel sides. Unlike regular quadrilaterals like squares and rectangles, irregular quadrilaterals can look very different from each other. Their angles and side lengths can change quite a bit.

Characteristics of Irregular Quadrilaterals

Irregular quadrilaterals have some key features that set them apart from regular ones:

No Equal Sides: All four sides can have different lengths.
No Parallel Sides: There are no pairs of opposite sides that run parallel.
Varied Angles: The angles can be different; however, all their angles together still add up to 360 degrees.

These traits make irregular quadrilaterals quite diverse in shape.

Examples and Diagrams

Let’s look at some examples of irregular quadrilaterals:

A kite: It has two pairs of adjacent sides that are equal but is not considered regular.
An arbitrary trapezoid: While some trapezoids have one pair of parallel sides, others do not.

Examples of Irregular Quadrilaterals

You can find irregular quadrilaterals in everyday life. Here are some places you might see them:

Buildings: Many have windows shaped like irregular polygons.
Road signs: Some use unusual shapes to stand out better.

Check out these examples you might notice around you:

A diamond-shaped sign
An oddly cut piece of paper
Certain artistic designs

These examples show how unique and varied these shapes can be based on size and angles.

Properties of Irregular Quadrilaterals

To understand the properties of irregular shapes, it’s good to know about their angles and side lengths:

Angles: No matter what the shape looks like, the total will always be 360 degrees.
Side Lengths: Each side can be a different length with no restrictions, unlike regular shapes like parallelograms or trapezoids where specific relationships exist.

While both regular and irregular quadrilaterals share basic traits as four-sided figures, their differences come mainly from symmetry and uniformity. Understanding these shapes is important for classifying geometric shapes accurately!

Quadrilateral Properties at a Glance

Type of Quadrilateral	Opposite Sides	Opposite Angles	All Angles	Sides	Diagonals
Parallelogram	Equal	Equal	Sum = 360°	2 pairs equal	Bisect each other
Rectangle	Equal	Equal	Each = 90°	Opposite sides equal; all angles right	Equal and bisect each other
Square	Equal	Equal	Each = 90°	All sides equal	Equal and bisect each other
Rhombus	All sides equal	Congruent	Sum = 360°	All sides equal	Bisect but unequal lengths
Trapezoids	One pair is parallel	Can vary	Sum = 360°	Two pairs unequal	No specific rules

Detailed Descriptions for Each Type

Parallelograms: A parallelogram has two pairs of opposite sides that are the same length. The angles opposite each other are also the same. For example, if one angle is 60°, the one across will also be 60°. Remember, all four angles in any quadrilateral add up to 360°.

Rectangles: Rectangles have four corners that form right angles, meaning each corner measures 90 degrees. Like parallelograms, they also have opposite sides that are equal in length. An extra cool thing about rectangles is their diagonals are always the same length!

Squares: A square is a special type of rectangle. It has all four sides equal in length and every angle is a right angle. Plus, its diagonals not only match in length but they cross each other at right angles.

Rhombuses: Rhombuses look similar to squares and rectangles since they have two pairs of parallel sides. What makes them unique is that all four sides are the same length, while their angles can be different. The opposite angles are still equal though.

Trapezoids: Trapezoids are a bit different because they only have one pair of parallel sides. They can take on different forms, such as an isosceles trapezoid where the non-parallel sides (or legs) are the same length. The sum of all angles still adds up to 360°, just like any quadrilateral.

Visual Representation

Diagrams would really help show these shapes and their properties better! Seeing how they look helps understand how the properties fit together.

Understanding these types of quadrilaterals helps show how they’re connected in geometry. While some share features like having parallel or equal-length sides, others stand out with special traits like unique angle measures or side lengths. So whether you’re studying for school or just curious, knowing about quadrilaterals opens up a neat world of shapes!

Classifying Quadrilaterals

Classifying quadrilaterals means knowing their features. A quadrilateral is a shape with four sides. There are many types of quadrilaterals, each with its own traits. The main types include parallelograms, rectangles, squares, trapezoids, and kites.

Step-by-Step Process for Classifying Quadrilaterals

To classify different quadrilaterals, follow these steps:

Identify the Sides: Check if it has four sides.
Examine Parallel Sides:
- Parallelogram: Both pairs of opposite sides are equal and parallel.
- Rectangle: Like a parallelogram, but it also has four right angles (90 degrees).
- Square: All sides are equal and all angles are right angles; it’s a special type of rectangle.
- Trapezoid: Has only one pair of parallel sides.
Check Angles:
- Use a protractor to see if any angle measures 90 degrees for rectangles or squares.
Look at Side Lengths:
- For kites, check if two pairs of adjacent sides are equal in length.

By observing these properties—like angles and side lengths—you can figure out which type your shape belongs to.

Example Problems

Here are some example problems that ask you to classify shapes based on their properties:

If you have a shape with two pairs of opposite sides that are both equal and parallel—what type is this?
What about a shape that has only one pair of parallel sides—how would you classify it?
Consider a figure where all four sides are the same length but not all angles are right; what classification fits best?

Here’s a table to help clarify these examples:

Type	Properties
Parallelogram	Opposite sides equal & parallel
Rectangle	Four right angles
Square	All sides equal & four right angles
Trapezoid	One pair of parallel sides
Kite	Two pairs of adjacent equal-length sides

Encourage students to explain why they classified each shape based on its features.

Area, Perimeter, and Angles

Area Calculations for Different Quadrilaterals

To find the area of different quadrilaterals, we use specific formulas. Each type of quadrilateral has its own way to calculate the area.

Parallelogram:
Area = base × height
Rectangle:
Area = length × width
Square:
Area = s²
where s is the length of one side.
Trapezoid:
Area = (Base₁ + Base₂) / 2 × h
Base₁ and Base₂ are the lengths of the two parallel sides. h is the height between them.

Example Calculation

Let’s calculate some areas:

For a parallelogram with a base of 10 units and height 5 units:
Area = 10 × 5 = 50 square units.
For a rectangle measuring 8 units in length and 4 units in width:
Area = 8 × 4 = 32 square units.
For a square with each side measuring 6 units:
Area = 6² = 36 square units.
For a trapezoid with bases measuring 6 and 10 units, and a height of 4 units:
Area = (6 + 10) / 2 × 4 = (16 / 2) × 4 = 32 square units.

These examples show how to apply these formulas clearly.

Perimeter Calculations for Different Quadrilaterals

To find the perimeter of any quadrilateral, you add up all its side lengths. Here’s how it works:

General Formula:
To find the perimeter (P):
P = side₁ + side₂ + side₃ + side₄.

Examples:

In an irregular quadrilateral with sides measuring 5, 7, 9, & 12 units:
Perimeter = P = 5 + 7 + 9 + 12 = 33 units.

For regular shapes like rectangles or squares:

Rectangle: If it has length (l) = 8 unit and width (w) = 3 unit, then
P = (l + w) × 2 = (8 + 3) × 2 = 22 unit.
Square: If each side measures s = 5 unit:
P = s × 4 => 20 unit.

Angle Calculations in Quadrilaterals

Angles in quadrilaterals have special rules. The sum of interior angles in any four-sided figure is always 360°.

To find unknown angles, follow these steps:

Add together known angle measures.
For example, if three angles measure 90°, 80°, and 70°:
[90° + 80° + 70° = 240°] Now subtract from 360° to find the fourth angle:
[360° − 240° = 120°]
So, the fourth angle must be 120°.

This method works for many types like kites or trapezoids too!

FAQs About Quadrilaterals

What are similar quadrilaterals?

Similar quadrilaterals have the same shape but different sizes. Their corresponding angles are equal, and their sides are proportional.

What are congruent quadrilaterals?

Congruent quadrilaterals are exactly the same in size and shape. All corresponding sides and angles match perfectly.

What is a right trapezoid?

A right trapezoid has one angle that measures 90 degrees. This angle forms a right angle with one of its bases.

What are parallel lines in quadrilaterals?

Parallel lines never meet. They maintain equal distance apart throughout their lengths.

What is line symmetry in quadrilaterals?

Line symmetry means a shape can be folded along a line to create mirror images on both sides.

How do adjacent sides differ from opposite sides in quadrilaterals?

Adjacent sides meet at a vertex, while opposite sides do not touch each other.

How can I use quadrilateral worksheets for practice?

Worksheets provide exercises for identifying types, calculating areas, and solving problems related to quadrilaterals.

Additional Key Topics on Quadrilaterals

Mathematical Shapes: Understand various shapes used in geometry.
Geometric Properties: Explore properties such as symmetry, angles, and side relationships.
Math Education: Use educational resources for teaching and learning about shapes.
Polygon Classification: Learn how to classify different polygons, including quadrilaterals.
Practice Problems: Engage with exercises that focus on identifying and calculating aspects of quadrilaterals.
Angle Measurements: Study interior angles and their sums in different types of quadrilaterals.
Coordinate Geometry of Quadrilaterals: Investigate how coordinates can define shapes in a plane.
Applications of Quadrilaterals: Discover real-life scenarios where these shapes appear in architecture or design.